
Figure 1: Two-bending process experiment and measurements.
The Negative Gravitational Force in
Plant Growth Dynamics
Wendy Lin
Class 2015, International Section
The High School Affiliated to Renmin University of China
Beijing 10080, China
2015-01-15
Abstract
Higher plants respond to gravitropism, e.g., a horizontally placed stem will bend upwards at a certain position. This phenomenon was discovered by Knight in 1806 and had been studied by Darwin in 1880. As early as 1882, Sachs proposed a sine law for modeling, which stated that the component of gravity acting at right angle to a plant axis determines the strength of the gravitropic response. The sine law took the plant¡¯s gravity component to drive its bending and it is now widely used for its simplicity. However, it has also faced difficulties to model complicated problems. In this paper we first presented two experiments using Arabidopsis plants, one was a two-bending process to measure the bending position, the other was an in-homogeneous growing test. Based on experimental observations, we proposed a new theory in which the plant bending and normal growth are driven by the same engine of an upward ¡°negative gravitational force¡±. The force is independent of gravity and inhomogeneously distributed along the stem axis, from highest value at the apex and decreasing as going away. When the stem is placed horizontally, this force will work with the downward gravity to cause a maximum moment value at a certain point of the stem, making the stem bend there. Thus, this theory will provide a fundamentally different new view to plant growth dynamics and solve more complicated problems.
Keywords: gravitropism, stimulus, movement, Arabidopsis
Significance Statement
The traditional sine law takes only a single gravity component as the driving factor, thus it faces various difficulties in gravitropic modeling, such as explaining where a bending point occurs in a horizontally placed stem. This paper has proposed a fundamentally different theory, in which gravitropism is driven by an upward, inhomogeneously distributed ¡°negative gravitational force¡±, which is also independent of gravity. When the stem is placed horizontally, this theory can determine a maximum moment point in the stem, which accords with the bending point location in experiments. Therefore, this theory will provide a more accurate modeling to plant growth dynamics.
1. Introduction
It is well known that higher plants respond to gravitropism, in which shoots grow upwards and roots grow downwards. This topic has received great attention since Knight (1) in 1806 and Darwin (2) in 1880. Many experiments regarding gravitropism of Arabidopsis thaliana have been reported, e.g., by Masson et al (3) and Fukaki et al (4). As early as 1882, Sachs (5) proposed a sine law to model the plant growth process, which was commented by Dumais (6) that the component of gravity perpendicular to a stem axis determines the strength of stimulus. The sine law model has been widely used so far. However, its shortcomings have also been reported recently, e.g. see Bastiena et al (7), who proposed an improvement by eliminating the zigzag phenomenon in the modeling.
A basic experiment for gravitropism is to put a plant, e.g. Arabidopsis, down horizontally, to observe the stem bend upwards at a certain position. In this case, the components of gravity perpendicular to a stem are equal for all stem segments along the axis, which makes the bending strength of the stimulus homogeneously distributed. Since the sine law takes only the plant¡¯s gravity component as the driving factor, it faces difficulty to predict where Arabidopsis stems bend exactly and explain why a certain position is chosen to bend when the plant responds to gravitropism.
The purpose of this work is to provide a fundamentally different theory to gravitropic modeling. There were two experiments in this work. The first experiment was designed with a two-bending process. First, the plant was put down horizontally for one day to allow the stem to bend upwards about 90 degrees at a certain spot. Then, the plant was put back vertically for another day so the stem would bend upwards again. As a result, one could see that two bending points appeared on the plant stem. It is a question why the first bending did not take place at the apex or basal end, and why the stem had a second bending point, instead of bending back in the first point to recover its original straight shape. Then, in the second experiment, the Arabidopsis stem was marked in several places. The length increasement of each part was measured after 4 days in order to study the distribution of stimulus along the stem. Based on experimental observations, this paper introduces a new plant growth dynamics theory, in which the plant bending and normal growth are driven by the same engine of an upward ¡°negative gravitational force¡±. The force is independent of gravity and inhomogeneously distributed along the stem axis. When the stem is horizontally placed, this force will work with the downward gravity to cause a maximum moment value at a certain point of the stem, making the stem bend at that point. This analysis agrees well with the phenomena observed during the Arabidopsis experiments.
2. The Two-Bending Process Experiment
The experiment was designed with a two-bending process for Arabidopsis plants. A standard procedure of planting and transplanting was conducted to prepare the plant specimens. When a seedling grew into a shoot and bolted to at least 4 cm, a picture was taken with a scale to record the original length of the stem, as shown in the Day1 picture of Figure 1. Then the flower pot was put down horizontally and placed for 24 hrs. Another picture was taken to record the first bending of the stem, as shown in the Day2 picture of Figure 1. Then, the flower pots were placed vertically once again for another 24 hrs. A picture was taken to record the second bending of the stem, as in Day3 of Figure 1.

Figure 1: Two-bending process experiment and measurements.
During the experiment, the lengths of different sections of the shoot were measured. As shown in Figure 1, the Day1 length of the whole stem, from top to bottom was denoted by A. In Day2, two extended lines of the bended stem were drawn beyond the point of intersection, creating an angle. The angle bisector intersected stem at point P, which is supposedly the middle of the bended arc. The length from point P to the stem bottom was represented by B. Also in Day2, the stem length from the top of the shoot to point P was represented by a, which would be used as the reference length in the second bending. In the Day3 picture, the same process was used to find point Q. The curve length from point P to Q was represented by b. With these definitions, both A and a represented original lengths of the stem. B and b both represented parts of the stem that supposedly did not grow during the bending process. Thus ratios B/A and b/a represented the relative positions of bending points P and Q on the stem.
Experiments were conducted using the techniques above. The numbers of replicates were 34 for Arabidopsis Wild Type (Col0), 39 for DR5 GFP. Figure 2 to 3 show the measurements for (A,B) and (a,b) for two types of the plants. It is seen that (A,B) and (a,b) show a close linear relationship.
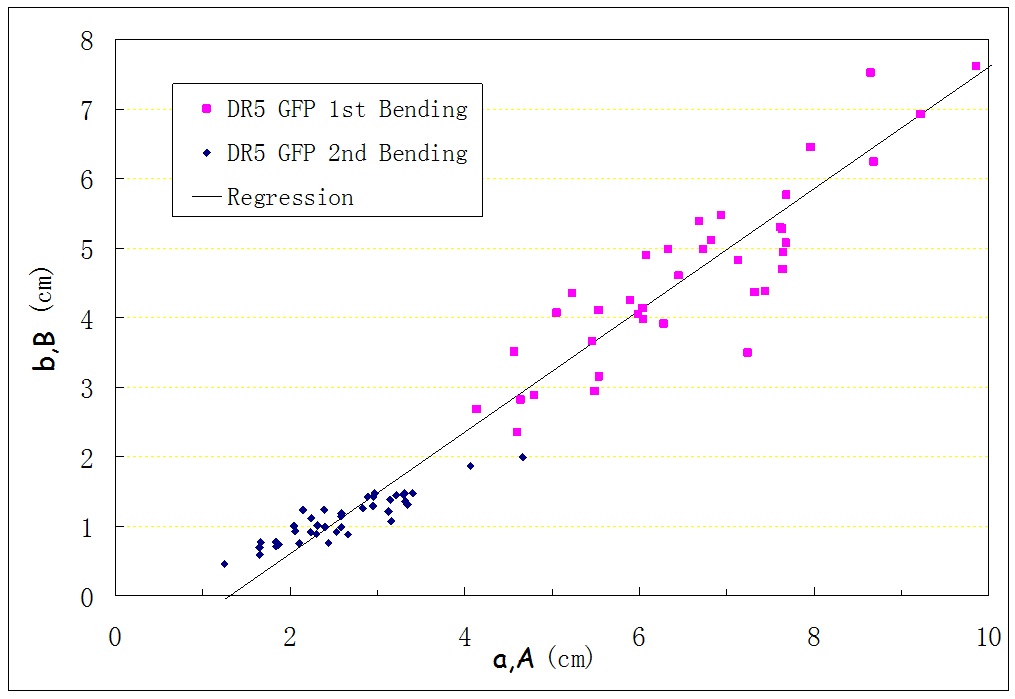
Figure 2: Plotted points for Arabidopsis Wild Type.
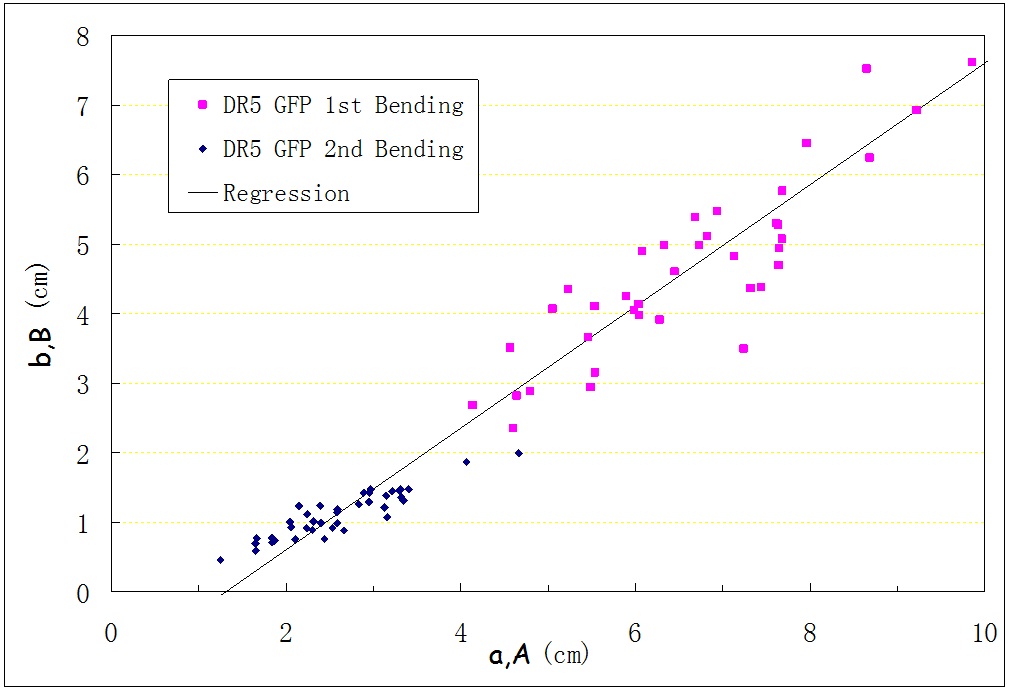
Figure 3: Plotted Points for DR5 GFP.
Through a large amount of experiments, we can get the following conclusion: The first bending point is far from the basal end (B/A is around 0.7), and during the second bending process, a distinguished second bending point Q appears which has a distance of b from the first bending point P (b/a is around 0.3 to 0.5). The first bending never took place at the apex or basal end (B not equal to 0 or A), and the stem always had a second bending point (b not equal to 0), instead of bending back in the first point to recover its original straight shape.
3. The Experiment on Inhomogeneously Growing Stem
The preparation for this experiment was the same as that of the previous one. However, plants were not put horizontally. Instead, in Day1, the stem was marked by black ink in different places. This idea came from Fukaki et al (4), however we did not study the curvatures of stem sections. A photo was taken to measure the length of each stem section, as shown in Day1 of Figure 4. Then, the plant was kept in a normal vertical state for 4 days. In Day5, another photo was taken to measure the lengths of each stem section again, as shown in Figure 4. In order to analyze the experimental data, suppose a stem section had the length of L1 in Day1, and L5 in Day5. The relative increasement (L5¨CL1)/L1 was calculated, and plotted with x, the original distance from shoot tip to the center of stem section, as shown in Figure 5.

Figure 4: Measurement of an inhomogeneously growing stem.
We assume that the plant¡¯s bending and normal growth are driven by the same engine of stimulus in the stem. It is seen from the picture that the growths of each stem section were not equal. The nearer to the apex, the longer the stem section grew. This means, if the gravitropism in an Arabidopsis stem was initiated by a stimulus, then the stimulus distribution along the stem was not homogeneous. The nearer to the apex, the stronger the stimulus was, and it became weaker the farther away from the tip.
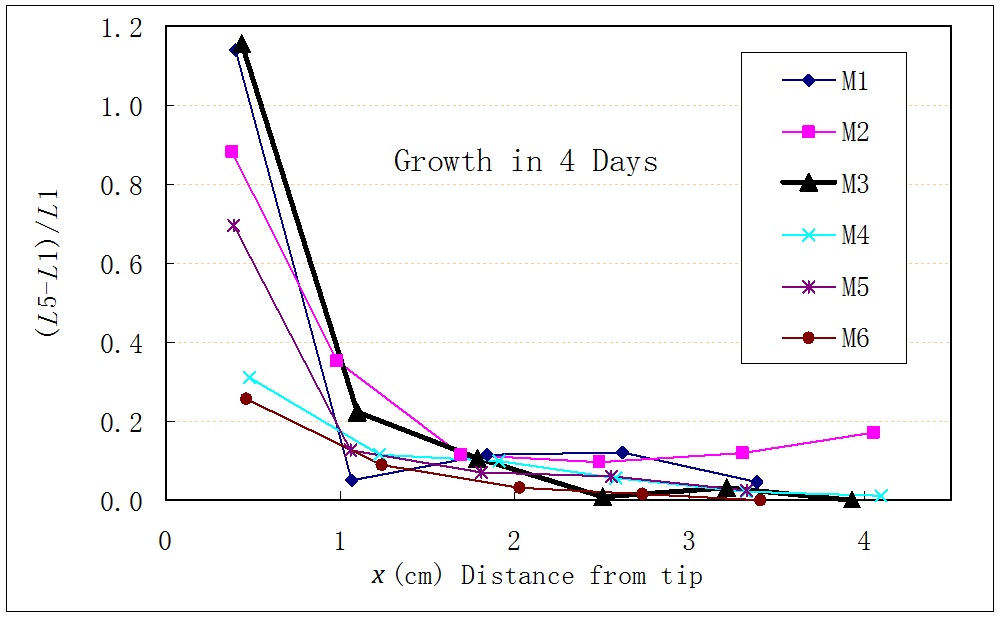
Figure 5: Relative increasement of the stem section versus the distance from the apex.
4. The Formulation of Negative Gravitational Force
A common theory to model a plant¡¯s gravitropism is the sine law proposed by Sachs (5) in 1882, which states that the component of gravity acting at a right angle to a plant axis determines the strength of the stimulus for shoots to curve up. The sine law has been used for over a century, but its restriction has caused much attention recently, see Dumais (6), and Bastiena et al (7). For a horizontally placed stem, the gravity component is homogeneous along the axis. Thus the sine law also faces difficulty to explain why the shoot chooses to bend up at a particular spot.
We can see as evidence in the experiment that during the bending process only a small curving part took a large deformation, while most of the stem had little or no change in shape. Instead, it took a movement of rotation and translation. According to Newton¡¯s First Law, for movements and shape changes in the curving part of the stem to happen, the plant must be acted upon by external forces. Since one of the external forces is gravity, the stem must also be subjected to an upward force in order to curve upwards. A stem segment undergoing large deformation must be subjected to a bigger action of bending, while those undergoing rotation and translation may be subjected to less bending.
Negative gravitropism in Arabidopsis reveals the existence of a ¡°negative gravitational force¡±. This is a force that the Earth applies on plants, and it deviates from the Earth¡¯s core (i.e. in opposite direction of gravity). According to the second experiment above, if a stimulus is the major source of gravisensing, and it is much more concentrated on the shoot tip than the stem sections farther away from the apex, one may conclude that the strength of the negative gravitational force is strongest around the apex region. The farther away from the apex, the weaker the strength of the negative gravitational force will be, and so the negative gravitational force must be inhomogeneous. Also, the stimulus always exists in the stem regardless of its vertical or horizontal position. Thus, the magnitude of the upward component of the ¡°negative gravitational force¡± remains unchanged when the stem is put down horizontally.
Without losing generality, we¡¯ll focus on the second bending point Q. Suppose that we use an ideal Arabidopsis thaliana plant with a stem perpendicular to the ground. In Figure 6(a) below, when the plant is put down horizontally, the first bending point is P with an ideal curvature angle of 90 degrees. Once the plant is put back vertically, the stem from the tip of the shoot 0 (\(x\)=0) to point P is ideally parallel to the ground with a length of \(a\). Q is the second bending point, QP having a length of \(b\). As an ideal case, suppose the stem part 0P is subjected to a linearly distributed egative gravitational force \[ f(x) = \frac{p}{a} (a-x) \] which is pointing upwards. The function \(f(x)\) is assumed to be strongest at the tip \(x = 0\), and zero in the first bending point \(x = a\), which is in consistent with experimental observation. Also, suppose line 0P is subjected to a homogeneously distributed gravity, which has a load density of \(mg/a\) per unit length, where \(m\) is the mass of the shoot part 0P, and \(g\) is the gravitational acceleration.
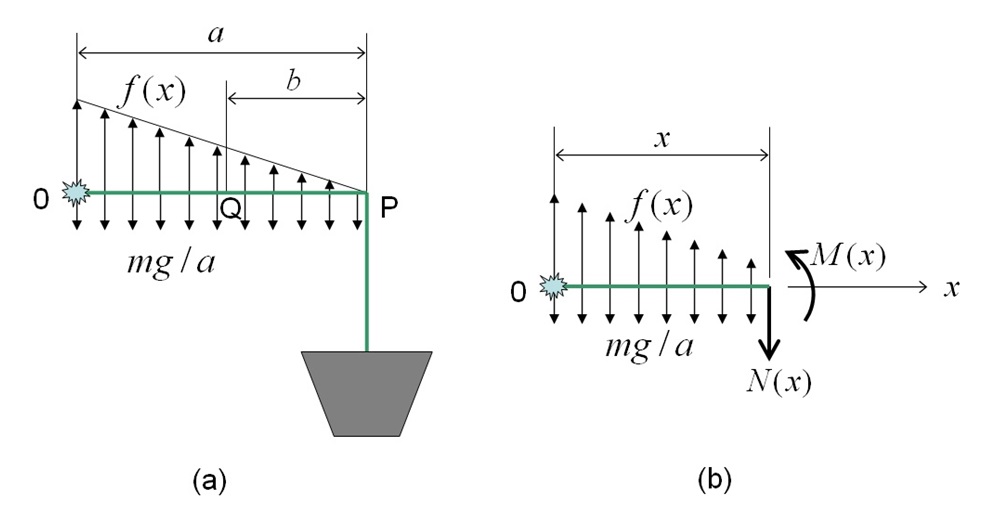
Figure 6: A force diagram for an ideal Arabidopsis plant.
In Figure 6(b), the plant stem is cut at any point \(x\) between 0 and P, leaving us with a stem length of \(0x = x\). An inner force \(N(x)\) and an inner moment \(M(x)\) are added to the cross section to keep the shoot in balance. Physically, it is easy to infer that \(M(x)\) has a maximum value at the bending point Q.
We calculate the moments of all forces to a given point \(x\). According to the static equilibrium condition, the sum of that should be zero, \[ M(x)+N(x)\cdot 0 - \int^x_0 (x-\xi)\cdot \frac{p}{a} (a-\xi) {\rm d}\xi + \int^x_0 (x-\xi)\cdot \frac{mg}{a} {\rm d}\xi = 0 \] After finishing integration, we have, \[ M(x) = p \cdot \Big( \frac{1}{2} x^2 - \frac{1}{6a} x^3 \Big) - \frac{mg}{2a} x^2 \] The function \(M(x)\) is a cubic polynomial, which will have a maximum value at a point \(x\). A general form of the cubic polynomial can be seen in Figure 7 below with three assumed parameters.
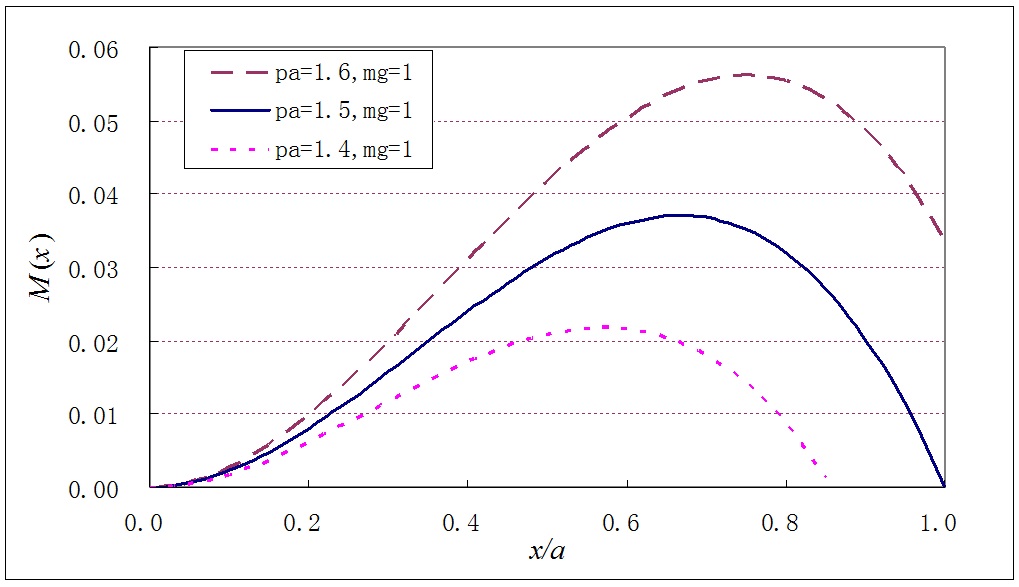
Figure 7: A general form of the moment function.
The fact that the moment function has a maximum value accords with the Arabidopsis stem having a bending point \(x_m = a-b\). This is also proof that an inhomogeneous negative gravitational force exists. Let us take a derivative on the moment function with respect to variable \(x\), \[ M'(x) = p\Big(1-\frac{x}{2a} \Big) x - \frac{mg}{a} x \] If the bending point \(x_m = a-b\) is set to be the maximum point of moment \(M(x)\), then \( M'(a-b) = 0\) . Thus the magnitude of the negative gravitational force at apex can be measured from experiments, i.e. \[ p = \frac{2mg}{a+b} \] where, \(m\) is the mass of the stem horizontally placed, and \(g\) is the gravitational acceleration.
Besides the maximum point at \(x_m = a-b \), the moment function curve with a parameter of \(pa > 1.5\) is very promising, since it has a high value at boundary \(x = a\), i.e. the first bending point P. This well explains why the angle at point P increased and the stem segment PQ bended upwards during the second bending process, as seen in Figures 1.
Although the analysis above was taken under ideal circumstances, it should be a good approximation for general plants. For a stem placed with an arbitrary angle, the magnitude of the upward component of the ¡°negative gravitational force¡± will be the same. Thus the moment on the stem section can be calculated using the same approach and its movements can also be modeled. Therefore, compared to the sine law, this theory has provided a better approach to solve more complicated problems in plant growth dynamics.
5. Conclusion
This work has presented two experiments for plant gravitropism. One was a two-bending process experiment to observe the bending position; the second one was an inhomogeneous growing test to measure the stimulus distribution. Based on the experimental data, this paper has introduced a new plant growth dynamics theory, in which the plant¡¯s bending and normal growth are driven by the same engine of an upward ¡°negative gravitational force¡±. The force is independent of gravity and inhomogeneously distributed along the stem axis, from highest value at the apex and decreasing when going away. When the stem is placed horizontally, this force will work with the downward gravity to cause a maximum moment value at some point of the stem, making the stem bend at that point. Thus, this theory will provide a fundamentally different new view to the plant growth dynamics, and solve more complicated problems.
Acknowledgement. I would like to thank my biology teacher, Dr. LI Feng for supervising me in doing this project. I would like to thank Professor WANG Donghui of the School of Life Sciences at Peking University for providing me with excellent laboratory equipments to conduct the experiments, and also giving me many helpful suggestions.
References